
Myeloid lineage commitment and differentiation of hematopoietic and myeloid progenitors are orchestrated by myeloid-lineage-specific growth factors ( Boettcher and Manz, 2017, Mossadegh-Keller et al., 2013, Sarrazin and Sieweke, 2011) and cytokines, such as interleukin (IL)-1β ( Pietras et al., 2016). HSPCs are able to respond to stress, such as severe infection, systemic inflammation, or iatrogenic myeloablation, by increasing their proliferation rate and hematopoiesis ( Trumpp et al., 2010, Zhao and Baltimore, 2015). Hematopoiesis is a hierarchical system, in which hematopoietic stem and progenitor cells (HSPCs) are responsible for its maintenance via their differentiation into progressively committed progenitors and mature cells ( Trumpp et al., 2010). We have, thus, hypothesized that the adaptive processes induced by trained immunity involve alterations to progenitors of the hematopoietic system, a concept that has not been addressed yet. However, the long-term effects (up to months) of trained immunity on circulating monocytes are puzzling, as these cells have a relatively short lifespan in the circulation.
Transcriptomic and metabolomic analysis have implicated metabolic pathways, especially glucose metabolism, in the adaptation of monocytes and macrophages in the context of innate immune memory ( Arts et al., 2016a, Arts et al., 2016b, Cheng et al., 2014, Netea et al., 2016). Pathogen-associated molecular patterns or cytokines induce a complex immunometabolic program in monocytes and macrophages, enabling a robust cellular response to re-stimulation, especially with regard to cytokine production ( Arts et al., 2016a, Netea et al., 2016, Quintin et al., 2012). This process involves changes in cell transcription and is designated “trained immunity” ( Goodridge et al., 2016, Jensen et al., 2015, Netea and van Crevel, 2014, Netea et al., 2016, Quintin et al., 2012). Recent studies have shown that certain microbial challenges or vaccines promote a heightened response of myeloid cell populations to a subsequent infection with the same or even different pathogens. Therefore, modulation of myeloid progenitors in the bone marrow is an integral component of trained immunity, which to date, was considered to involve functional changes of mature myeloid cells in the periphery. The trained-immunity-related increase in myelopoiesis resulted in a beneficial response to secondary LPS challenge and protection from chemotherapy-induced myelosuppression in mice. Administration of β-glucan (prototypical trained-immunity-inducing agonist) to mice induced expansion of progenitors of the myeloid lineage, which was associated with elevated signaling by innate immune mediators, such as IL-1β and granulocyte-macrophage colony-stimulating factor (GM-CSF), and with adaptations in glucose metabolism and cholesterol biosynthesis. We thus hypothesized that trained immunity acts via modulation of hematopoietic stem and progenitor cells (HSPCs). But really unless you are in a production environment the time spent on further analysis is not really cost effective given how fast this executes as it is.Trained innate immunity fosters a sustained favorable response of myeloid cells to a secondary challenge, despite their short lifespan in circulation. It is quite obvious that the desired root is close to $x=170$, so starting with $0$ as the left hand limit for the bisection can be improved. The solution method can be improved somewhat if you send some time analysing the problem. If ff(a,Nknots)*y > tic,MyMain(100,1e-12),tocĬhanging from n=100 to n=10000 in Simpson's rule less than doubles the computational time required. So if I understand this correctly, we need to use Simpson's rule to evaluate $x_l$ where
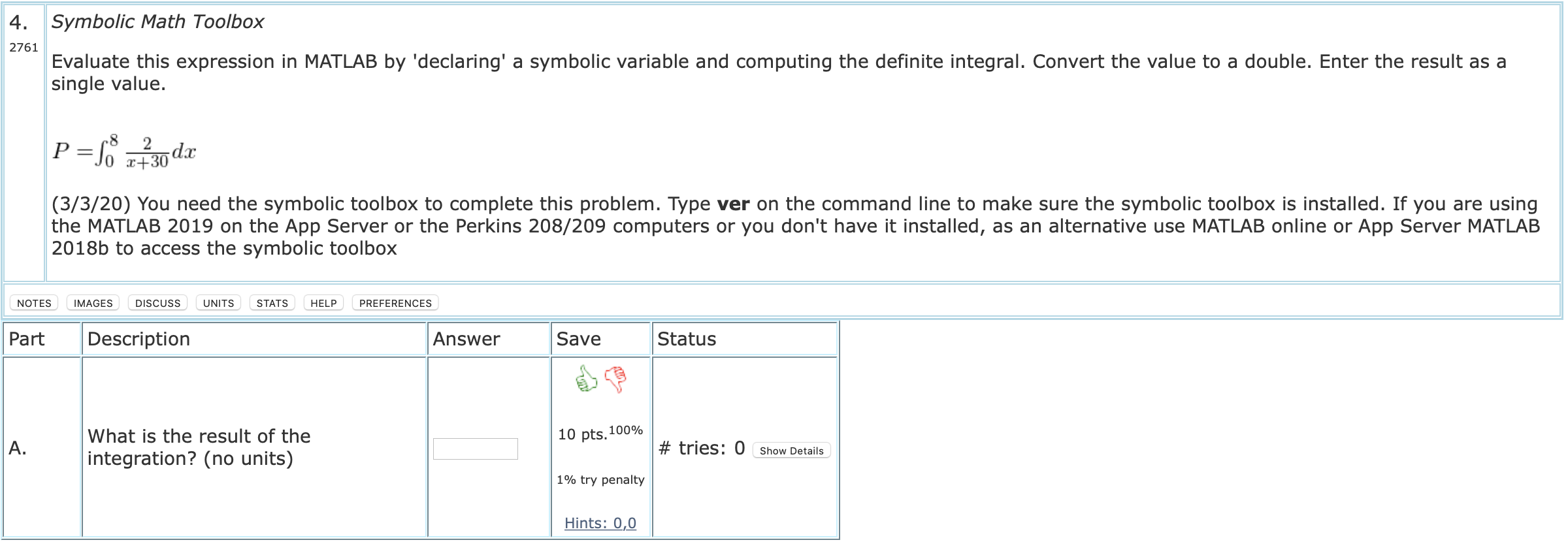
When $R=200$ and $L=170.$ Evaluate all the integrals by using the composite Simpson's rule. Use Matlab and numerical methods to find $x_l$ so that


 0 kommentar(er)
0 kommentar(er)
